8 Modules¶

8.1 Définition¶

Les modules sont des programmes Python qui contiennent des fonctions que l'on est amené à réutiliser souvent (on les appelle aussi bibliothèques ou libraries). Ce sont des « boîtes à outils » qui vont vous être très utiles.

Les développeurs de Python ont mis au point de nombreux modules qui effectuent une quantité phénoménale de tâches. Pour cette raison, prenez toujours le réflexe de vérifier si une partie du code que vous souhaitez écrire n'existe pas déjà sous forme de module.

La plupart de ces modules sont déjà installés dans les versions standards de Python. Vous pouvez accéder à une documentation exhaustive sur le site de Python. N'hésitez pas à explorer un peu ce site, la quantité de modules disponibles est impressionnante (plus de 300).

8.2 Importation de modules¶

Dans les chapitres précédents, nous avons rencontré la notion de module plusieurs fois. Notamment lorsque nous avons voulu tirer un nombre aléatoire :

>>> import random
>>> random.randint(0, 10)
4

Regardons de plus près cet exemple :

Ligne 1, l'instruction import donne accès à toutes les fonctions du module random.
Ensuite, ligne 2, nous utilisons la fonction randint(0, 10) du module random. Cette fonction renvoie un nombre entier tiré aléatoirement entre 0 inclus et 10 inclus.

Nous avons également croisé le module math lors de l'exercice sur la spirale (voir chapitre 7 Fichiers). Ce module nous a donné accès aux fonctions trigonométriques sinus et cosinus, et à la constante $\pi$ :

>>> import math
>>> math.cos(math.pi / 2)
6.123233995736766e-17
>>> math.sin(math.pi / 2)
1.0

En résumé, l'utilisation de la syntaxe import module permet d'importer tout une série de fonctions organisées par « thèmes ». Par exemple, les fonctions gérant les nombres aléatoires avec random et les fonctions mathématiques avec math. Python possède de nombreux autres modules internes (c'est-à-dire présent de base lorsqu'on installe Python).

Remarque

Dans le chapitre 3 Affichage, nous avons introduit la syntaxe truc.bidule() avec truc étant un objet et .bidule() une méthode. Nous vous avions expliqué qu'une méthode était une fonction un peu particulière :

elle était liée à un objet par un point ;
en général, elle agissait sur ou utilisait l'objet auquel elle était liée.

Par exemple, la méthode .format() (vue au chapitre 3) dans l'instruction "{}".format(3.14) utilise l'objet chaîne de caractères "{}" (auquel elle est liée) pour finalement renvoyer une autre chaîne de caractères "3.14".

Avec les modules, nous rencontrons une syntaxe similaire. Par exemple, dans l'instruction math.cos(), on pourrait penser que .cos() est aussi une méthode. En fait la documentation officielle de Python précise bien que dans ce cas .cos() est une fonction. Dans cet ouvrage, nous utiliserons ainsi le mot fonction lorsqu'on évoquera des fonctions issues de modules.

Si cela vous parait encore ardu, ne vous inquiétez pas, c'est à force de pratiquer et de lire que vous vous approprierez le vocabulaire. Ici, la syntaxe module.fonction() est là pour rappeler de quel module provient la fonction en un coup d’œil !

Il existe un autre moyen d'importer une ou plusieurs fonctions d'un module :

>>> from random import randint
>>> randint(0,10)
7

À l'aide du mot-clé from, on peut importer une fonction spécifique d'un module donné. Remarquez bien qu'il est inutile de répéter le nom du module dans ce cas, seul le nom de la fonction en question est requis.

On peut également importer toutes les fonctions d'un module :

>>> from random import *
>>> randint(0,50)
46
>>> uniform(0,2.5)
0.64943174760727951

L'instruction from random import * importe toutes les fonctions du module random. On peut ainsi utiliser toutes ses fonctions directement, comme par exemple randint() et uniform() qui renvoie des nombres aléatoires entiers et floats.

Dans la pratique, plutôt que de charger toutes les fonctions d'un module en une seule fois :

from random import *

nous vous conseillons de charger le module seul de la manière suivante :

import random

puis d'appeler explicitement les fonctions voulues, par exemple :

random.randint(0,2)

Il est également possible de définir un alias (un nom plus court) pour un module :

>>> import random as rand
>>> rand.randint(1, 10)
6
>>> rand.uniform(1, 3)
2.643472616544236

Dans cet exemple, les fonctions du module random sont accessibles via l'alias rand.

Enfin, pour vider de la mémoire un module déjà chargé, on peut utiliser l'instruction del :

>>> import random
>>> random.randint(0,10)
2
>>> del random
>>> random.randint(0,10)
Traceback (most recent call last):
  File "<stdin>", line 1, in ?
NameError: name 'random' is not defined

On constate alors qu'un rappel (ligne 5) d'une fonction du module random après l'avoir vidé de la mémoire (ligne 4) retourne un message d'erreur (lignes 6-8).

8.3 Obtenir de l'aide sur les modules importés¶

Pour obtenir de l'aide sur un module rien de plus simple, il suffit d'utiliser la commande help() :

>>> import random
>>> help(random)
[...]

Ce qui renvoie quelque chose du type :

Help on module random:

NAME
    random - Random variable generators.

MODULE REFERENCE
    https://docs.python.org/3.7/library/random

    The following documentation is automatically generated from the Python
    source files.  It may be incomplete, incorrect or include features that
    are considered implementation detail and may vary between Python
    implementations.  When in doubt, consult the module reference at the
    location listed above.

DESCRIPTION
    integers
    --------
           uniform within range

    sequences
    ---------
           pick random element
           pick random sample

Remarque

Pour vous déplacer dans l'aide, utilisez les flèches du haut et du bas pour parcourir les lignes les unes après les autres, ou les touches page-up et page-down pour faire défiler l'aide page par page.
Pour quitter l'aide, appuyez sur la touche Q.
Pour chercher du texte, tapez le caractère / puis le texte que vous cherchez puis la touche Entrée. Par exemple, pour chercher l'aide sur la fonction randint(), tapez /randint puis Entrée.
Vous pouvez également obtenir de l'aide sur une fonction particulière d'un module de la manière suivante :

help(random.randint)

La commande help() est en fait une commande plus générale permettant d'avoir de l'aide sur n'importe quel objet chargé en mémoire.

>>> t = [1, 2, 3]
>>> help(t)
Help on list object:

class list(object)
 |  list() -> new list
 |  list(sequence) -> new list initialized from sequence's items
 |  
 |  Methods defined here:
 |  
 |  __add__(...)
 |      x.__add__(y) <==> x+y
 |  
...

Enfin, pour connaître d'un seul coup d’œil toutes les méthodes ou variables associées à un objet, utilisez la fonction dir() :

>>> import random
>>> dir(random)
['BPF', 'LOG4', 'NV_MAGICCONST', 'RECIP_BPF', 'Random', 'SG_MAGICCONST',
'SystemRandom', 'TWOPI', 'WichmannHill', '_BuiltinMethodType', '_MethodT
ype', '__all__', '__builtins__', '__doc__', '__file__', '__name__', '_ac
os', '_ceil', '_cos', '_e', '_exp', '_hexlify', '_inst', '_log', '_pi',
'_random', '_sin', '_sqrt', '_test', '_test_generator', '_urandom', '_wa
rn', 'betavariate', 'choice', 'expovariate', 'gammavariate', 'gauss', 'g
etrandbits', 'getstate', 'jumpahead', 'lognormvariate', 'normalvariate',
 'paretovariate', 'randint', 'random', 'randrange', 'sample', 'seed', 's
 etstate', 'shuffle', 'uniform', 'vonmisesvariate', 'weibullvariate']
>>>

8.4 Quelques modules courants¶

Il existe une série de modules que vous serez probablement amenés à utiliser si vous programmez en Python. En voici une liste non exhaustive. Pour la liste complète, reportez-vous à la page des modules sur le site de Python :

math : fonctions et constantes mathématiques de base (sin, cos, exp, pi...).
sys : interaction avec l'interpréteur Python, passage d'arguments (cf. plus bas).
os : dialogue avec le système d'exploitation (cf. plus bas).
random : génération de nombres aléatoires.
time : accès à l'heure de l'ordinateur et aux fonctions gérant le temps.
urllib : récupération de données sur internet depuis Python.
Tkinter : interface python avec Tk. Création d'objets graphiques (cf. chapitre 20 Fenêtres graphiques et Tkinter).
re : gestion des expressions régulières (cf. chapitre 16 Expressions régulières et parsing*).

Nous vous conseillons d'aller explorer les pages de ces modules pour découvrir toutes leurs potentialités.

Vous verrez dans le chapitre 14 Création de module comment créer votre propre module lorsque vous souhaitez réutiliser souvent vos propres fonctions.

Enfin, notez qu'il existe de nombreux autres modules externes qui ne sont pas installés de base dans Python mais qui sont très utilisés en bioinformatique et en analyse de données. Citons-en quelques-uns: NumPy (manipulations de vecteurs et de matrices, algèbre linéaire), Biopython (recherche dans les banques de données biologiques, manipulation de séquences ou de structures de biomolécules), matplotlib (représentations graphiques : courbes, nuages de points, diagrammes en bâtons...), pandas (analyse de données)... Ces modules vous serons présentés dans le chapitre 17 Quelques modules d'intérêt en bioinformatique.

8.5 Module random : génération de nombres aléatoires¶

Comme indiqué précédemment le module random contient des fonctions pour la génération de nombres aléatoires :

>>> import random
>>> random.randint(0, 10)
4
>>> random.randint(0, 10)
10
>>> random.uniform(0, 10)
6.574743184892878
>>> random.uniform(0, 10)
1.1655547702189106

Le module random permet aussi de permuter aléatoirement des listes :

>>> x = [1, 2, 3, 4]
>>> random.shuffle(x)
>>> x
[2, 3, 1, 4]
>>> random.shuffle(x)
>>> x
[4, 2, 1, 3]

Mais aussi de tirer alétoirement un ou plusieurs éléments dans une liste donnée :

>>> bases = ["A", "T", "C", "G"]
>>> random.choice(bases)
'A'
>>> random.choice(bases)
'G'
>>> random.choices(bases, k=5)
['G', 'A', 'A', 'T', 'G']
>>> random.choices(bases, k=5)
['A', 'T', 'A', 'A', 'C']
>>> random.choices(bases, k=10)
['C', 'T', 'T', 'T', 'G', 'A', 'C', 'A', 'G', 'G']

La fonction choice() tire aléatoirement un élément d'une liste alors que choices() (avec un s à la fin) réalise plusieurs tirages aléatoires, dont le nombre est précisé par le paramètre k.

Si vous exécutez vous-même les exemples précédents, vous devriez obtenir des résultats légèrement différents de ceux indiqués. C'est l'intérêt de l'aléatoire !

Pour des besoins de reproductibilité des analyses en science, on a souvent besoin de retrouver les mêmes résultats même si on utilise des nombres aléatoires. Pour cela, on peut définir ce qu'on appelle la « graine aléatoire ».

Définition

En informatique, la généreration de nombres aléatoires est un problème complexe. On utilise plutôt des « générateurs de nombres pseudo-aléatoires ». Pour cela, une graine aléatoire doit être définie. Cette graine est la plupart du temps un nombre entier qu'on passe au générateur, celui-ci va alors produire une série donnée de nombres pseudo-aléatoires qui dépendent de cette graine. Si on change la graine, la série de nombres change.

En Python, la graine aléatoire se définit avec la fonction seed() :

>>> random.seed(42)
>>> random.randint(0, 10)
1
>>> random.randint(0, 10)
0
>>> random.randint(0, 10)
4

Ici la graine aléatoire est fixée à 42. Si on ne précise pas la graine, par défaut Python utilise la date. Plus précisément, il s'agit du nombre de secondes écoulées depuis une date donnée du passé. Ainsi, à chaque fois qu'on relance Python, la graine sera différente car ce nombre de secondes sera différent.

Si vous exécutez ces mêmes lignes de code (depuis l'instruction random.seed(42)), il se peut que vous ayez des résultats différents selon la version de Python. Néanmoins, vous devriez systématiquement obtenir les mêmes résultats si vous relancez plusieurs fois de suite ces instructions sur une même machine.

Remarque

Quand on utlise des nombres aléatoires, il est fondamental de connaitre la distribution de probablités utilisée par la fonction. Par exemple, La fonction de base du module random est random.random(), elle renvoie un float aléatoire entre 0 et 1 tiré dans une distribution uniforme. Si on tire beaucoup de nombres, on aura la même probabilité d'obtenir tous les nombres possibles entre 0 et 1. La fonction random.randint() tire aussi un entier dans une distribution uniforme. La fonction random.gauss() tire quant à elle un float aléatoire dans une distribution Gaussienne.

8.6 Module sys : passage d'arguments¶

Le module sys contient des fonctions et des variables spécifiques à l'interpréteur Python lui-même. Ce module est particulièrement intéressant pour récupérer les arguments passés à un script Python lorsque celui-ci est appelé en ligne de commande.

Dans cet exemple, créons le court script suivant que l'on enregistrera sous le nom test.py :

import sys
print(sys.argv)

Ensuite, dans un shell, exécutons le script test.py suivi de plusieurs arguments. Par exemple :

$ python test.py salut girafe 42
['test.py', 'salut', 'girafe', '42']

Ligne 1. Le caractère $ représente l'invite du shell, test.py est le nom du script Python, salut, girafe et 42 sont les arguments passés au script (tous séparés par un espace).

Ligne 2. Le script affiche le contenu de la variable sys.argv. Cette variable est une liste qui contient tous les arguments de la ligne de commande, y compris le nom du script lui-même qu'on retrouve comme premier élément de cette liste dans sys.argv[0]. On peut donc accéder à chacun des arguments du script avec sys.argv[1], sys.argv[2]...

Toujours dans le module sys, la fonction sys.exit() est utile pour quitter un script Python. On peut donner un argument à cette fonction (en général une chaîne de caractères) qui sera renvoyé au moment où Python quittera le script. Par exemple, si vous attendez au moins un argument en ligne de commande, vous pouvez renvoyer un message pour indiquer à l'utilisateur ce que le script attend comme argument :

import sys

if len(sys.argv) != 2:
    sys.exit("ERREUR : il faut exactement un argument.")

print(f"Argument vaut : {sys.argv[1]}")

Puis on l'exécute sans argument :

$ python test.py
ERREUR : il faut exactement un argument.

et avec un argument :

$ python test.py 42
Argument vaut : 42

Notez qu'ici on vérifie que le script possède deux arguments car le nom du script lui-même compte pour un argument (le tout premier).

L'intérêt de récupérer des arguments passés dans la ligne de commande à l'appel du script est de pouvoir ensuite les utiliser dans le script.

Voici à titre d'exemple le script compte_lignes.py qui va prendre comme argument le nom d'un fichier puis afficher le nombre de lignes qu'il contient.

import sys

if len(sys.argv) != 2:
    sys.exit("ERREUR : il faut exactement un argument.")

nom_fichier = sys.argv[1]
taille = 0
with open(nom_fichier, "r") as f_in:
    taille = len(f_in.readlines())

print(f"{nom_fichier} contient {taille} lignes.")

Supposons que dans le même répertoire, nous ayons le fichier zoo1.txt dont voici le contenu :

girafe
tigre
singe
souris

et le fichier zoo2.txt qui contient :

poisson
abeille
chat

Utilisons maintenant notre script compte_lignes.py :

$ python compte_lignes.py
ERREUR : il faut exactement un argument.
$ python compte_lignes.py zoo1.txt
zoo1.txt contient 4 lignes.
$ python compte_lignes.py zoo2.txt
zoo2.txt contient 3 lignes.

Notre script est donc capable de :

Vérifier si un argument lui est donné et si ce n'est pas le cas d'afficher un message d'erreur.
D'ouvrir le fichier dont le nom est fourni en argument, de compter puis d'afficher le nombre de lignes.

Par contre, le script ne vérifie pas si le fichier existe bien :

$ python compte_lignes.py zoo3.txt
Traceback (most recent call last):
 File "compte_lignes.py", line 8, in <module>
   with open(nom_fichier, "r") as f_in:
FileNotFoundError: [Errno 2] No such file or directory: 'zoo3.txt'

La lecture de la partie suivante va nous permettre d'améliorer notre script compte_lignes.py.

8.7 Module os : interaction avec le système d'exploitation¶

Le module os gère l'interface avec le système d'exploitation.

La fonction os.path.exists() est une fonction pratique de ce module qui vérifie la présence d'un fichier sur le disque dur.

>>> import sys
>>> import os
>>> if os.path.exists("toto.pdb"):
...     print("le fichier est présent")
... else:
...     sys.exit("le fichier est absent")
...
le fichier est absent

Dans cet exemple, si le fichier n'existe pas sur le disque, on quitte le programme avec la fonction exit() du module sys que nous venons de voir.

La fonction os.getcwd() renvoie le répertoire (sous forme de chemin complet) depuis lequel est lancé Python :

>>> import os
>>> os.getcwd()
'/home/pierre'

Enfin, la fonction os.listdir() renvoie le contenu du répertoire depuis lequel est lancé Python :

>>> import os
>>> os.listdir()
['1BTA.pdb', 'demo.py', 'tests']

Le résultat est renvoyé sous forme d'une liste contenant à la fois le nom des fichiers et des répertoires.

Il existe de nombreuse autres fonctions dans le module os, n'hésitez pas à consulter la documentation.

8.8 Exercices¶

Conseils : pour les trois premiers exercices, utilisez l'interpréteur Python. Pour les exercices suivants, créez des scripts puis exécutez-les dans un shell.

8.8.1 Racine carrée¶

Affichez sur la même ligne les nombres de 10 à 20 (inclus) ainsi que leur racine carrée avec 3 décimales. Utilisez pour cela le module math avec la fonction sqrt(). Exemple :

10 3.162
11 3.317
12 3.464
13 3.606
[...]

Documentation de la fonction math.sqrt() :

https://docs.python.org/fr/3/library/math.html#math.sqrt

8.8.2 Cosinus¶

Calculez le cosinus de $\pi/2$ en utilisant le module math avec la fonction cos() et la constante pi.

Documentation de la fonction math.cos() :

https://docs.python.org/fr/3/library/math.html#math.cos

Documentation de la constante math.pi :

https://docs.python.org/fr/3/library/math.html#math.pi

8.8.3 Nom et contenu du répertoire courant¶

Affichez le nom et le contenu du répertoire courant (celui depuis lequel vous avez lancé l'interpréteur Python).

Déterminez également le nombre total de fichiers et de répertoires présents dans le répertoire courant.

Documentation de la fonction os.getcwd() :

https://docs.python.org/fr/3/library/os.html#os.getcwd

Documentation de la fonction os.listdir() :

https://docs.python.org/fr/3/library/os.html#os.listdir

8.8.4 Affichage temporisé¶

Affichez les nombres de 1 à 10 avec 1 seconde d'intervalle. Utilisez pour cela le module time et sa fonction sleep().

Documentation de la fonction time.sleep() :

https://docs.python.org/fr/3/library/time.html#time.sleep

8.8.5 Séquences aléatoires de chiffres¶

Générez une séquence aléatoire de 6 chiffres, ceux-ci étant des entiers tirés entre 1 et 4. Utilisez le module random avec la fonction randint().

Documentation de la fonction random.randint() :

https://docs.python.org/fr/3/library/random.html#random.randint

8.8.6 Séquences aléatoires d'ADN¶

Générez une séquence aléatoire d'ADN de 20 bases de deux manières différentes. Utilisez le module random avec la fonction randint() ou choice().

Documentation de la fonction random.randint() :

https://docs.python.org/fr/3/library/random.html#random.randint

Documentation de la fonction random.choice() :

https://docs.python.org/fr/3/library/random.html#random.choice

8.8.7 Séquences aléatoires d'ADN avec argument¶

Créez un script dna_random.py qui prend comme argument un nombre de bases, construit une séquence aléatoire d'ADN dont la longueur est le nombre de bases fourni en argument, puis affiche cette séquence.

Le script devra vérifier qu'un argument est bien fourni et renvoyer un message d'erreur si ce n'est pas le cas.

Conseil : pour générer la séquence d'ADN, vous utiliserez, au choix, la fonction
random.randint() ou random.choice() abordées dans l'exercice précédent.

8.8.8 Compteur de lignes¶

Améliorez le script compte_lignes.py dont le code a été donné précédemment de façon à ce qu'il renvoie un message d'erreur si le fichier n'existe pas. Par exemple, si les fichiers zoo1.txt et zoo2.txt sont bien dans le répertoire courant, mais pas zoo3.txt :

$ python compte_lignes.py zoo1.txt
zoo1.txt contient 4 lignes.
$ python compte_lignes.py zoo2.txt
zoo2.txt contient 3 lignes.
$ python compte_lignes.py zoo3.txt
ERREUR : zoo3.txt n'existe pas.

8.8.9 Détermination du nombre pi par la méthode Monte Carlo (exercice +++)¶

Soit un cercle de rayon 1 (en trait plein sur la figure 1) inscrit dans un carré de côté 2 (en trait pointillé).

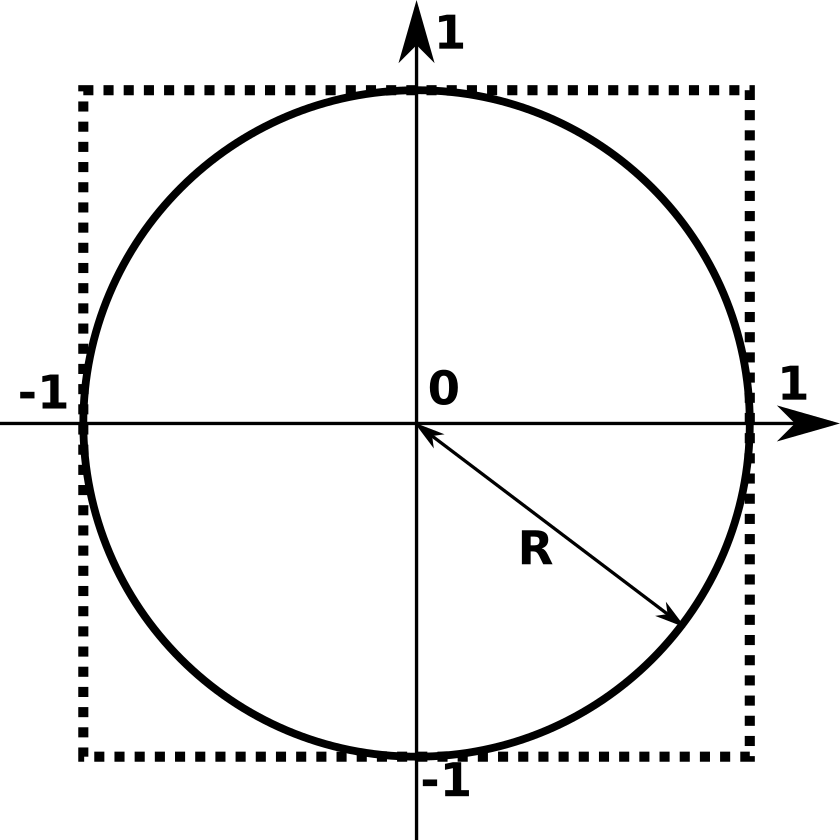
Cercle de rayon 1 inscrit dans un carré de côté 2.

Figure 1. Cercle de rayon 1 inscrit dans un carré de côté 2.

Avec $R = 1$, l'aire du carré vaut $(2R)^2$ soit 4 et l'aire du disque délimité par le cercle vaut $\pi R^2$ soit $\pi$.

En choisissant $N$ points aléatoires (à l'aide d'une distribution uniforme) à l'intérieur du carré, la probabilité que ces points se trouvent aussi dans le cercle est :

\[ p = \frac{\mbox{aire du cercle}}{\mbox{aire du carré}} = \frac{\pi}{4} \]

Soit $n$, le nombre de points effectivement dans le cercle, il vient alors

\[ p = \frac{n}{N} = \frac{\pi}{4}, \]

d'où

\[ \pi = 4 \times \frac{n}{N}. \]

Déterminez une approximation de $\pi$ par cette méthode. Pour cela, pour $N$ itérations :

Choisissez aléatoirement les coordonnées x et y d'un point entre -1 et 1. Utilisez la fonction uniform() du module random.
Calculez la distance entre le centre du cercle et ce point.
Déterminez si cette distance est inférieure au rayon du cercle, c'est-à-dire si le point est dans le cercle ou pas.
Si le point est effectivement dans le cercle, incrémentez le compteur \verb=n=.

Finalement calculez le rapport entre n et N et proposez une estimation de $\pi$. Quelle valeur de $\pi$ obtenez-vous pour 100 itérations ? 1000 itérations ? 10 000 itérations ? Comparez les valeurs obtenues à la valeur de $\pi$ fournie par le module math.

On rappelle que la distance d entre deux points A et B de coordonnées respectives $(x_A, y_A)$ et $(x_B, y_B)$ se calcule comme :

\[ d = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2} \]

Documentation de la fonction random.uniform() :

https://docs.python.org/fr/3/library/random.html#random.uniform